第七课 旋转变换
背景
接下来的变换是旋转变换,就是说给定一个角度和点,我们将点绕着一个坐标轴旋转。在旋转过程中发生变化的总是x,y,z三个坐标里面的其中两个,而不让第三个坐标值变化。这意味着,旋转路径总在三个坐标轴平面中的一个之中:绕 Z 轴的是 xy 面、绕 X 轴的是 yz 面、绕 Y 轴的是 xy 面。还有许多复杂的旋转变换可以让你绕任意一个向量旋转,但是眼下我们并不需要讨论这些。
让我们概括地定义这个问题这个问题。看看下面的这个图:
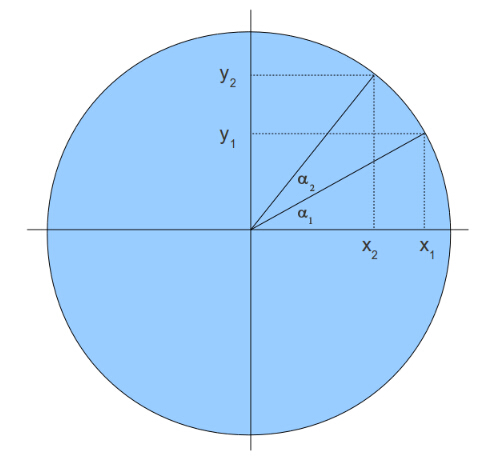
我们想沿着圆圈从(x1,y1)移动到(x2,y2)。也就是说我们让向量(x1,y1)转过a2角度。我们假设这个圆的半径是1。这意味着下列成立:
x1=cos(a1)
y1=sin(a1)
x2=cos(a1+a2)
y2=sin(a1+a2)
我们用下面的三角恒等式来产生 x2 和 y2 :
cos(a+b) = cosacosb - sinasinb
sin(a+b) = sinacosb+cosasinb
通过面的式子我们可以推导出:
x2=cos(a1+a2) = cosa1cosa2- sina1sina2 = x1cosa2- y1sina2
y2=sin(a1+a2) = sina1cosa2+ cosa1sina2 = y1cosa2+ x1sina2
在上面的图中我们看向 xy 平面,Z 轴指向屏幕内部!如果 X 分量和 Y 分量是四维向量的一部分,那样上面的等式可以写成下面的矩阵形式(不影响 Z 和 W )为:
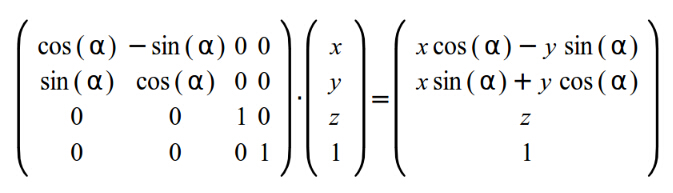
如果我们想创建一个绕着 Y 轴或者绕着 Z 轴的旋转变换矩阵,那么方程基本相同但是矩阵的安排却略有不同!这是绕Y轴旋转的矩阵:
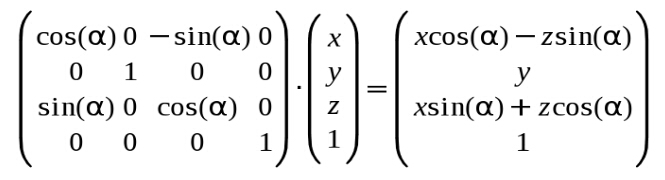
绕X轴的旋转矩阵为:
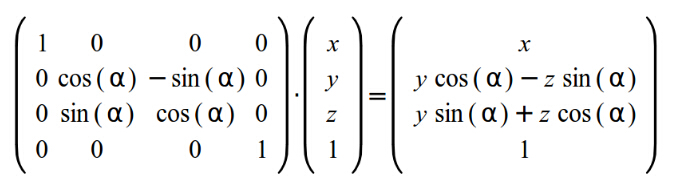
代码
在本节中程序的变化非常小,在编码中我们只改变其中旋转变换矩阵的内容:
World.m[0][0]=cosf(Scale); World.m[0][1]=-sinf(Scale);World.m[0][2]=0.0f; World.m[0][3]=0.0f;
World.m[1][0]=sinf(Scale); World.m[1][1]=cosf(Scale); World.m[1][2]=0.0f;World.m[1][3]=0.0f;
World.m[2][0]=0.0f; World.m[2][1]=0.0f; World.m[2][2]=1.0f; World.m[2][3]=0.0f;
World.m[3][0]=0.0f; World.m[3][1]=0.0f; World.m[3][2]=0.0f; World.m[3][3]=1.0f;正如你所看到的,通过上面的程序我们将绘制的三角形绕 Z 轴不断的旋转。你也可以尝试其他的旋转变换,但是我认为这时候由于没有真正的从3D到2D的投影变换,所以旋转看起来有点奇怪。我们将在之后的章节中用一个完整的变换管线类来完成他们。
操作结果